OpenSSL: 实战-RSA分段解密

简介

本篇是继 OpenSSL: 简单易上手的RSA加解密后的补充篇，实战篇。

在实际项目中，并没有像上篇文章写的那么简单，实际情况要复杂的多。万变不离其宗，抽丝剥茧，复杂事务的背后一定是有其本质原因和原理的存在，而我们就是挖掘原理，探索本质的福尔摩斯。

今天这篇文章，带领大家参与到实际项目中运用RSA加解密，在阅读下面内容之前，期望大家可以下载 openssl 的源码，或者下载我上篇文中的代码示例。

我下载的是 openssl-source-1.1.0f 这个版本的源码，正好对应我从 precompiled-openssl 下载的编译版本。

项目概述

该项目的开发语言仍然采用C语言来实现，我们借助 openssl 来模拟实际项目中的案例。

服务端使用 RSA 加密原始数据，然后采用 Base64 编码该加密数据经过 HTTP 传输给到客户端；

客户端接收到该数据，先使用 Base64 解码数据，然后再使用 RSA 解密数据，最终得到原始数据。

这里特别注意，客户端收到的数据大小可能会大于 128 字节，我们知道 RSA 加密明文最大长度 117 字节，而解密的最大值是 128 字节，所以超过该大小需要分段解密数据。

大概流程图如下：

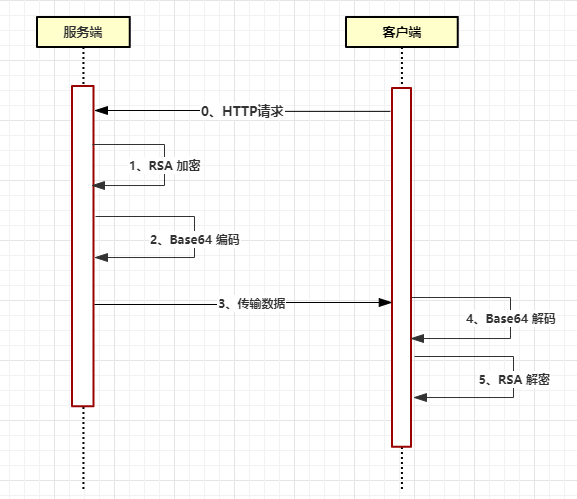
很简单的一个项目，对吧，接着往下看吧 :)-

解个小惑

也许有些朋友会问，为毛 RSA 加密的明文大小是 117 字节，而解密的最大字节数是 128 字节，两者一样不是更好吗，至少好理解呀？

得出上面结论的前提是我们RSA密钥长度是 1024 位即 128 字节（1024/8=128），同理如果是 512 位的密钥，那么最大的 RSA 解密字节长度应该是（512/8）64 字节，最大加密的明文长度是（64-11）53 字节。

在 openssl 源码中，我们可以看到如下代码：

1	# define RSA_PKCS1_PADDING_SIZE 11

在 rsa_sign.c 文件中可以看到 RSA_sign 函数：

int RSA_sign(int type, const unsigned char *m, unsigned int m_len,
             unsigned char *sigret, unsigned int *siglen, RSA *rsa)
{
    int encrypt_len, encoded_len = 0, ret = 0;
    unsigned char *tmps = NULL;
    const unsigned char *encoded = NULL;

    if (rsa->meth->rsa_sign) {
        return rsa->meth->rsa_sign(type, m, m_len, sigret, siglen, rsa);
    }

    /* Compute the encoded digest. */
    if (type == NID_md5_sha1) {
        /*
         * NID_md5_sha1 corresponds to the MD5/SHA1 combination in TLS 1.1 and
         * earlier. It has no DigestInfo wrapper but otherwise is
         * RSASSA-PKCS1-v1_5.
         */
        if (m_len != SSL_SIG_LENGTH) {
            RSAerr(RSA_F_RSA_SIGN, RSA_R_INVALID_MESSAGE_LENGTH);
            return 0;
        }
        encoded_len = SSL_SIG_LENGTH;
        encoded = m;
    } else {
        if (!encode_pkcs1(&tmps, &encoded_len, type, m, m_len))
            goto err;
        encoded = tmps;
    }

    if (encoded_len > RSA_size(rsa) - RSA_PKCS1_PADDING_SIZE) {
        RSAerr(RSA_F_RSA_SIGN, RSA_R_DIGEST_TOO_BIG_FOR_RSA_KEY);
        goto err;
    }
    encrypt_len = RSA_private_encrypt(encoded_len, encoded, sigret, rsa,
                                      RSA_PKCS1_PADDING);
    if (encrypt_len <= 0)
        goto err;

    *siglen = encrypt_len;
    ret = 1;

err:
    OPENSSL_clear_free(tmps, (size_t)encoded_len);
    return ret;
}

可以看出，RSA_PKCS1_PADDING 这种填充模式是占用了 11 个字节的，那么 127+11 正好也是 128 字节。

每次RSA加密的明文的长度是受RSA填充模式限制的，如下表：

填充方式	输入	输出	备注
RSA_PKCS1_PADDING	必须比RSA钥模长(modulus) 短至少11个字节, 也就是RSA_size(rsa) – 11，对于1024bit的密钥，RSA_size(rsa)=128字节，即明文为128-11=117字节；如果输入的明文过长，必须切割，然后填充。	和modulus一样长	最常用的填充方式
RSA_PKCS1_OAEP_PADDING	RSA_size(rsa) – 41	和modulus一样长	最优非对称填充OAEP，安全性是最高的
RSA_NO_PADDING	可以和RSA钥模长一样长，如果输入的明文过长，必须切割，然后填充。	和modulus一样长	-

这里注意下面结论：

在不同的padding模式下，使用相同长度的密钥可以加密的数据最大长度不同；
在不同密钥长度下，使用相同的padding模式可以加密的数据最大长度也不同；

可以阅读 rfc2313 中关于 PKCS #1: RSA Encryption Version 1.5 的部分。

开战

实战代码主要在 main.c 文件中的 example_rsa3() 函数中。

原始数据是字符串 www.veryitman.com，如下还包括了公私钥。

// 原始数据为字符串：www.veryitman.com
	unsigned char plainText[] = "www.veryitman.com";

	unsigned char publicKey[] = "-----BEGIN PUBLIC KEY-----\n"
		"MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgQCrPgCMJW17JN2DW7tZFk/FB6pU\n"
		"pLvLOo6G/EuND8XZptffXbyiY2VscMRhP+kKVeaLO9HuEYR3Zl78x8oR6prytstc\n"
		"/MueersWDxh4iGSHsZXGxA41hXrXLRElrSTRc43ea18o0zMxZoVZiR2JFt7QcgM+\n"
		"T6eOrvj59MhXv9O46QIDAQAB\n"
		"-----END PUBLIC KEY-----\n";

	unsigned char privateKey[] = "-----BEGIN RSA PRIVATE KEY-----\n"
		"MIICdgIBADANBgkqhkiG9w0BAQEFAASCAmAwggJcAgEAAoGBAKs+AIwlbXsk3YNb\n"
		"u1kWT8UHqlSku8s6job8S40Pxdmm199dvKJjZWxwxGE/6QpV5os70e4RhHdmXvzH\n"
		"yhHqmvK2y1z8y556uxYPGHiIZIexlcbEDjWFetctESWtJNFzjd5rXyjTMzFmhVmJ\n"
		"HYkW3tByAz5Pp46u+Pn0yFe/07jpAgMBAAECgYBj1YH8MtXhNVzveEuBZMCc3hsv\n"
		"vdq+YSU3DV/+nXN7sQmp77xJ8CjxT80t5VS38dy2z+lUImJYOhamyNPGHkC2y84V\n"
		"7i5+e6ScQve1gnwHqRKGBjtSCaYOqm9rTDECCTT1oMU26sfYznWlJqMrkJp1jWn7\n"
		"aAwr+3FcX2XhD74ZAQJBAN34Y6fmHLRPv21MsdgGqUjKgyFvJfLUmtFFgb6sLEWc\n"
		"k22J3BAFAcNCTLYHFZwMhL/nwaw9/7rIUJD+lcl6n3cCQQDFfrN14qKC3GJfoBZ8\n"
		"k9S6F7Ss514DDPzIuenbafhoUjZDVcjLw9EmYZQjpfsQ3WdNICUKRrDHZay1Pz+s\n"
		"YkKfAkB+OKfaquS5t/t/2LPsxuTuipIEqiKnMjSTOfYsidVnBEFlcZZc2awF76aV\n"
		"f/PO1+OJCO2910ebXBtMSCi++GbDAkEAmc7zNPwsVH4OnyquWJdJNSUBMSd/sCCN\n"
		"PkaMOrVtINHmMMq+dvMqEBoupRS/U4Ma0JYYQsiLJL+qof2AOWDNQQJAcquLGHLT\n"
		"eGDDLluHo+kkIGwZi4aK/fDoylZ0NCEtYyMtShQ3JmllST9kmb9NJX2gMsejsirc\n"
		"H6ObxqZPbka6UA==\n"
		"-----END RSA PRIVATE KEY-----\n";

对数据进行私钥加密，示例如下：

// 私钥加密
int encrypted_length = private_key_encrypt(plainText, len, privateKey, encrypted_str);
if (-1 == encrypted_length)
{
	printf("Private Encrypt failed\n");
	exit(0);
}

私钥加密之后，进行 Base64 编码：

char *base64_content;
size_t encrypted_str_length = strlen(encrypted_str);
int encode_res = mzc_base64_encode(encrypted_str, encrypted_str_length, &base64_content);
if (0 != encode_res)
{
	printf("Base64 encode failed\n");
	exit(0);
}
printf("Base64 encode content: %s\n\n", base64_content);
printf("Base64 encode content's length: %i\n\n", strlen(base64_content));

至此，上面两个步骤就模拟完成了服务端加密的过程。下面我们来继续模拟客户端解密的过程。

首先，对 Base64 编码之后的数据进行 Base64 解码。

char *base64DecodeOutput;
size_t decode_output_length;
int decode_res = mzc_base64_decode(base64_content, &base64DecodeOutput, &decode_output_length);
printf("base64 decode content: %s\n\n", base64DecodeOutput);
printf("base64 decode content's length: %i\n\n", decode_output_length);
if (0 != decode_res)
{
    printf("Base64 decode failed\n");
    exit(0);
}

看一下打印结果：

1	base64 decode content's length: 160

很明显，长度要大于 128，需要进行分段处理。

// 最大解密长度
#define RSA_MAX_DECRYPT_SIZE 128

// 每段解密的长度
int chunk = 0;
unsigned char tmp_dstr[RSA_MAX_DECRYPT_SIZE];
memset(tmp_dstr, '\0', sizeof(tmp_dstr));

// （数据被）分段解密（公钥解密）
while (chunk <= decode_output_length)
{
    int decrypted_length = public_key_decrypt(base64DecodeOutput, RSA_MAX_DECRYPT_SIZE, publicKey, tmp_dstr);
    memcpy(decrypted_str, tmp_dstr, decrypted_length);
    printf("Current decrypted content length =%d\n", decrypted_length);
    if (-1 == decrypted_length)
    {
        printf("Public Decrypt failed\n");
        exit(0);
    }
    chunk += decrypted_length;
}

printf("......\n\n");
printf("Final decrypted string =%s\n", decrypted_str);

输出结果：

1
2
3

......

Final decrypted string =www.veryitman.com

至此整个过程简单模拟结束。

大家如果感兴趣的话，可以实现分段加密的过程。我就不再演示这个过程了，后续加入到源代码中去。

问君能有几多愁，恰似一江春水向东流。